Frequency of family names

In five previous articles I talked about power-law distributions. I don’t know why I am so fond of them, but I do. Perhaps because I find them intriguing.

But while in all previous occasions I used power-laws to fit distributions related to networks, in this case I use them in connection with the frequency of family names. I looked up the frequencies of the most common family names in Italy, USA, Germany, and France (I also wanted to find Australia, but I didn’t find anything suitable). 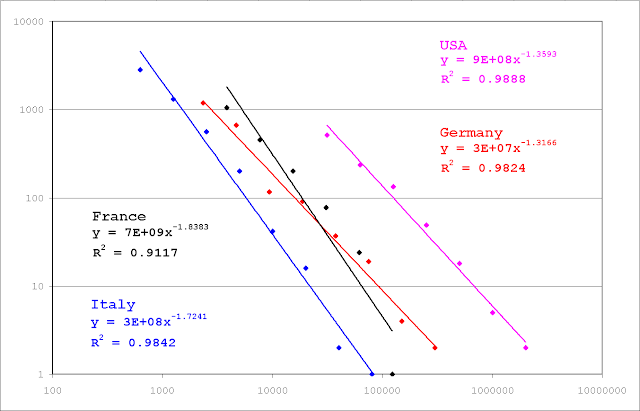Then, I binned the frequency in doubling intervals, so that they would appear uniform in a logarithmic scale, and plotted them with Excel. Here is what I got:

As you can see, France, with an index of 1.8383, shows the steepest slope, followed by Italy with 1.7241, USA with 1.3593, and Germany with 1.3166.

What does it mean? I don’t know. The slopes are quite close to each other, but those of countries with Latin-derived languages (France and Italy, 1.8 and 1.7) are steeper than those where Anglo-Saxon languages are spoken (USA and Germany, 1.4 and 1.3). Is this significant or is it only a coincidence?

I should do the same for Spanish, Portuguese, Rumanian (all Latin languages), and Dutch, Danish, and Swedish (all Anglo-Saxon).

And what about Slavonian languages like Russian, etc.?

Also, I had 4991 names for Italy, 2128 for Germany, 1818 for France, and 961 for USA. It would be interesting to see how sensitive the slopes are to the size of the samples.

These lists of names are probably derived from census data. It is inevitable that they will include foreign names in addition to the domestic ones. Has that a significant effect? In any case, America is a melting pot of immigrants from all over the world. How many American family names are actually of Anglo-Saxon origin?

In case you are curious, in my previous examples, the indices were 1.526 (Network of Feedbacks on eBay), 0.7262 (The small world of this blog), 1.1685 (More on visitors to this blog), and 1.2507 (A real small-world network #2).

I also had a further article on small-world networks but without power-law distributions (Small-world networks (or not?)).